
Louis Caves
Physicist/Engineer/Innovator/Dreamer
Email: louiscaves@gmail.com
Classical Mechanics
This is a simulation of a double pendulum system. See image to the right for a derivation of the equations of motion in Lagrangian Formalism. The video clip to the left is an animation of the system as a function of time for the parameters and initial conditions l1=l2=1 (length of pendulum arms), m1=m2=1 (masses of pendulum bobs), and theta_1=theta_2=pi (initial angle of pendulum bobs with respect to the -y axis). The solutions and simulations were coded using MATLAB. Source code can be found on my GitHub profile.

The double pendulum system will exhibit chaotic behavior, a mathematical phenomenon where a small change in the initial conditions of a system leads to a large difference in the trajectory at an arbitrary time t>0. The video clip to the left shows 5 different solutions where the initial position of the second bob vaires by 0.00001 radians.
Computational Fluid Dynamics
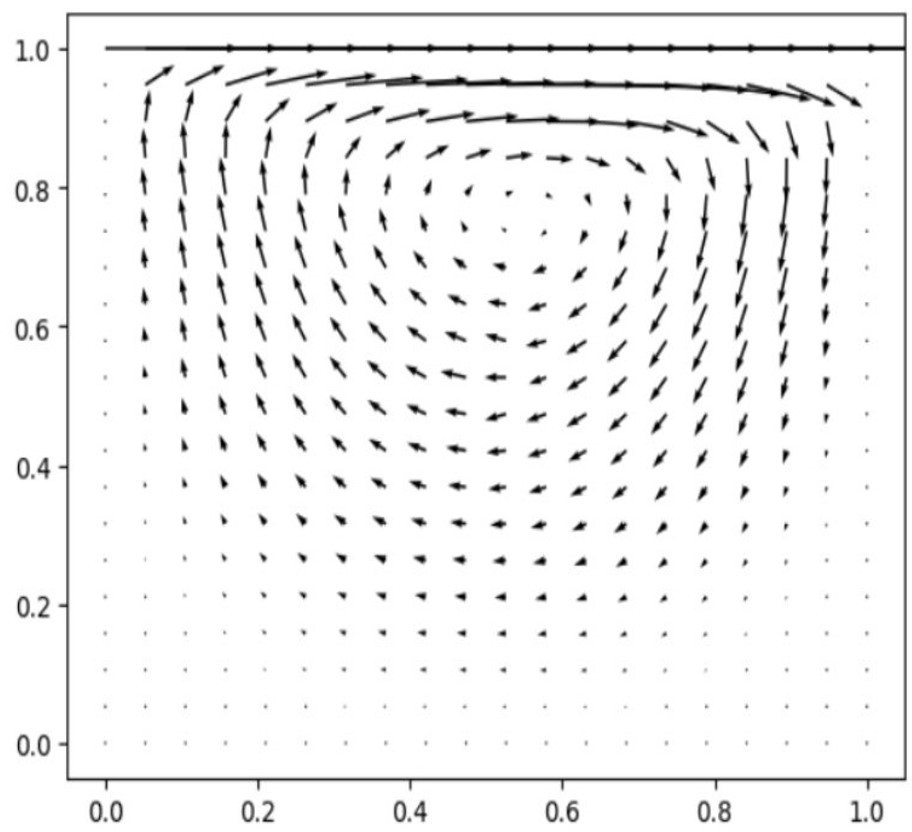
Here is a computational solution to the lid-driven cavity problem with a Reynolds number 50. The lid-driven cavity is a closed 2D box with the top surface moving at a constant speed U=1 and the rest of the walls are stationary. The solution on the left was generated using a first-order explicit finite difference scheme coded in Python (see source code). The solution on the right was generated using the open source CFD software OpenFOAM.
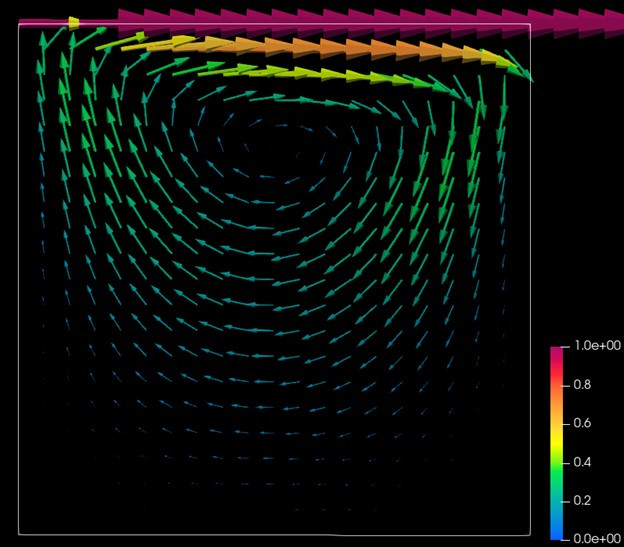

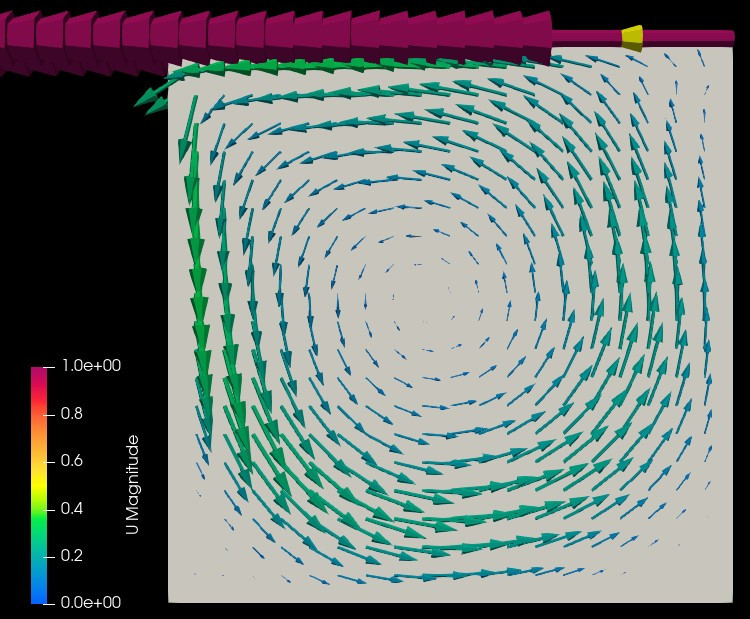
A Lid-Driven cavity-like device was created by passing a stream of water over a cavity of otherwise stationary fluid. The results are shown on the far left. The image in the center was created using a Reynolds averaged turbulent solver in openFOAM with a Reynolds number of 3000.
Astrodynamics
How does a smallsat with limited thrusting capability in an inclined low-earth orbit rendezvous with a larger satellite in a geostationary orbit? Slow and steady wins the race. Animations of orbital trajectory (left) and gound trace (right) are shown here. Full simulation files (coded in MATLAB) can be found on my GitHub page.